近年、放射線診断や放射線治療において、医用画像位置合わせは重要な技術になってきています。ここでは、医用画像解析に興味のある学生や研究者のために、医用画像位置合わせに必要な基礎知識についてまとめました。今回は、画像位置合わせに用いられる「画像の類似度の指標」を中心に紹介します。
2つの画像間で、片方の画像を移動、回転、変形させることにより、もう片方の画像に合わせこむ手法を画像位置合わせ(Registration)と言います。このRegistrationの技術は、医療現場において、様々なモダリティーから得られた画像の重ね合わせ(例えば、CT画像とMRI画像、MRI画像と PET画像など)に用いられています。
これらの画像の重ね合わせにより、ある組織においてCT画像では判別しにくい構造や機能をMRIやPET画像からより詳細に判別する、ということが可能になります(図1参照)。また、同一人物の別の日時に撮影された画像同士をRegistrationで合わせこむことによって、臓器がどのくらい変形・移動したかを見積もることができ、それらを考慮した診断・治療が可能となります。
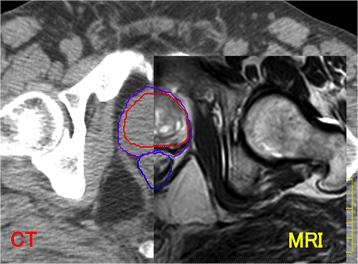
図中の紫色、赤色は、それぞれCT画像とMRI画像に基づいて囲まれた前立腺の領域。青色は、CT-MRI重ね合わせ画像に基づいて囲まれた直腸の領域 [1]
Registrationのアルゴリズムを端的に言えば、2つの画像の類似度を最大化するように、片方の画像に変換行列(ここでは並進、回転に限る)を施すということになります。
画像の類似度の指標(評価関数)
変換行列についての詳細は、また次回以降に述べることにして、今回は、画像間でのRegistrationに使われる画像の類似度の指標(評価関数)の代表的なものを紹介しようと思います。以下、2つの画像A(x)、B(x)において、A(x)を固定して、B(x)を変換行列TによってA(x)に向けてRegistrationする場合を考えます。B(x)の変換後の画像をB^T(x)と表します。
(ここで、xは画素の位置を表し、A(x)、B(x)、B^T(x)は画素値を表します。)では、類似度の評価関数を見ていきましょう。
1. 差分二乗和
(SSD:Sum of Squared Difference)
同じ位置の画素の画素値の差の2乗の総和で表され、値が0に近い程、類似度は高くなります。2つの画像の違いがガウシアンノイズ程度である時に適した指標です。

2. 差分絶対値和
(SAD : Sum of Absolute Difference)
同じ位置の画素の画素値の差の絶対値の総和で表され、SSDと同じく、値が0に近い程、類似度は高くなります。SSDに比べて、画素値に大きな違いがある画素(外れ値)の影響を受けにくい特徴があります。
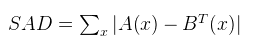
3. 正規化相互相関
(NCC: Normalized Cross-Correlation)

上式は、2つのベクトルの内積を表す式 、

の形になっています。そのため、類似度が高くなる程、値は1に近くなります。
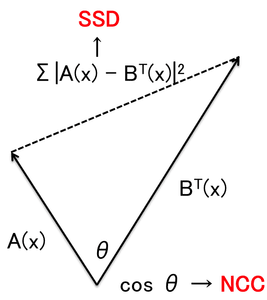
今、 A(x)とB^T(x) をL x M x N (pixel)の三次元画像とした場合、A(x)とB^T(x)は、L x M x N 個の画素の位置 x に対してそれぞれ画素値をもつ L x M x N 次元ベクトルと考えられます。そこで、SSDとNCCが意味するところをベクトル図で表すと図2のようになります。SSDは値が0に近づく程、NCCはθが0に近づく程、画像の類似度が高くなることが理解できると思います。
また、SSDはゲイン変動による画素値の変化(図2におけるベクトルの大きさの変化)の影響を受けるが、NCCはゲイン変動の影響を受けない(ベクトルのなす角度のみに依存するため)ことも理解できます。
NCCの改良版としてZNCC(Zero-mean Normalized Cross-Correlation)があります。これは、画像全体から全画素値の平均値を差し引いてから相互相関値を計算することによって、画像全体に乗っているノイズやバックグラウンドの影響を受けにくくなるという利点があります。そのため、NCCよりもZNCCの方が一般的によく用いられます。特に、2つの画像間で画像の明暗(バックグラウンド)に大きな差があるような場合には、ZNCCが用いられる場合が多いです。

但し、ZNCCをプログラミングする場合は、上記の式の通りに書くよりも、下記のように変形した形で書く方が効率の良いプログラムになります(上記のまま書くと、平均値を求める時と全画素から差し引く時の2回、全画素を参照することになるが、下記だと全画素の参照が一回で済むため)。

4. 画像均一度比
(Ratio image Uniformity)

と定義した時に、

RIUは、2つの画像間の画素値の比の標準偏差として定義され、値が0に近づく程、類似度は高くなります。
今回紹介した類似度の評価関数は、いずれも同一モダリティー画像間での位置合わせに使われることがほとんどです。異なるモダリティー画像間では、画素値の分布傾向が異なるため、単純に画素値の差や相関を類似度の評価関数として使用することはできません。
次回は、異なるモダリティー画像間での位置合わせに用いられる「相互情報量」という評価関数を紹介します。
【参考文献】
[1] Gianluca et al., Three-Tesla Magnetic Resonance and Computed Tomography Imaging in Three-Dimensional Conformal Radiotherapy for Localized Prostate Cancer, Open Journal of Radiology, Vol. 1, No. 1, pp.1-8 2011.
[2] Bailey, D.L. et al, Positron Emission Tomography: Basic Sciences, Springer, 2005.