CTはというと,既に完成された技術のように思いますが,「投影回数を少なくしたい」かつ,「様々な方向から投影できない」という場合にも対応できるように,より精密に断面を再構成する技術が求められています。
CTとは
CTとは,Computed Tomography の頭文字をとったもので,コンピュータ断層撮像法と訳されます。 CT検査とは,X線をつかって身体の断面を撮影する検査です。X線を照射し,断面を通過したデータを集め,画像処理を行うことで,断面を再構成します。
CTの応用分野は非常に広く,医療系であれば「カテーテルX線血管造影法」,「CTアンジオグラフィ」,「三次元欠陥撮影」(参考文献[1]),工業系であれば「非破壊検査」,「CAE」,「デジタルエンジニアリング」などがあります。
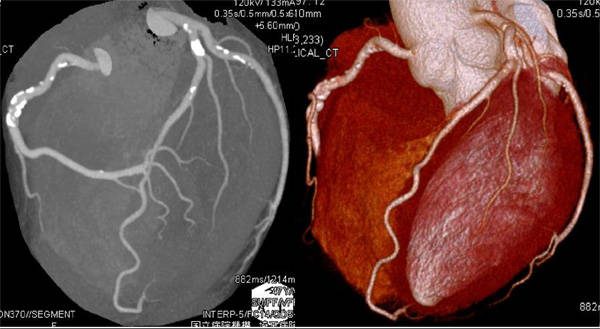
via saitama-hospital.jp
CTの原理
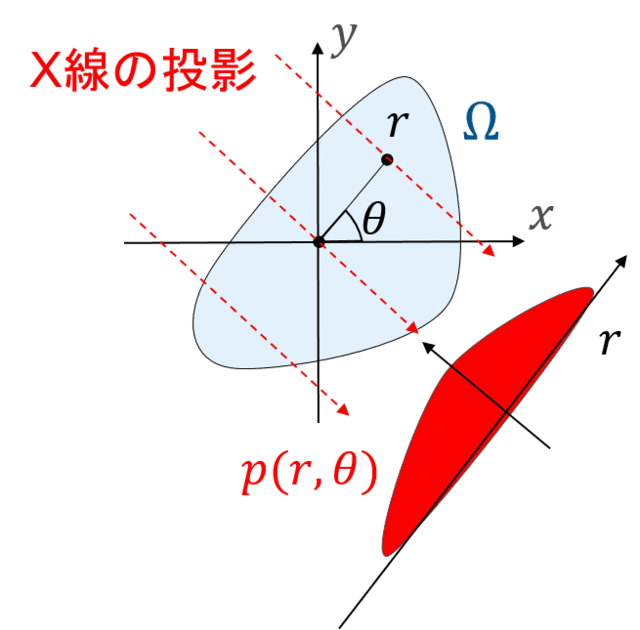
それではCTの原理について説明していきます。 CTは,X線を目的の物体に照射し,それの減衰を見ることによって,物体の形状を再構成する手法です. 投影する領域全体での減衰率f(x,y)f(x,y)を復元します. 図の角度θθからΩΩへ投影し,それにより得られる積分量は以下のように記述されます。
様々な角度θθからの投影により,f(x,y)f(x,y)を完全に求めることが目的です. このp(r,θ)p(r,θ)が観測量です。 関数p(r,θ)p(r,θ)をf(x,y)f(x,y)のラドン変換と呼びます。このδ(r)δ(r)というのはディラックのデルタ関数と呼ばれる関数であり,可積分な関数f(x)f(x) に対して
となるようなものです. δδの中身が00になるところだけ出現すると考えてもらってよいです。上での積分は,デルタ関数の定義から,物体をθθ方向から投影した総和が得られることがわかります。
Radon 変換のプログラム
以下,少しだけmatlab のコードを載せたいと思います。ラドン変換などの原理の理解の一助となれば幸いです。
まず,サンプルデータをロードします。
P = phantom(256);
imshow(P)
load_phantom.mat
次にラドン変換をします。
theta = 0:10:170; %% 投影する角度の設定
[R,xp] = radon(P,theta);
radon.matfigure, imagesc(theta,xp,R);
colormap(hot);
colorbar
xlabel('\theta');
ylabel('x\prime');
plot.mat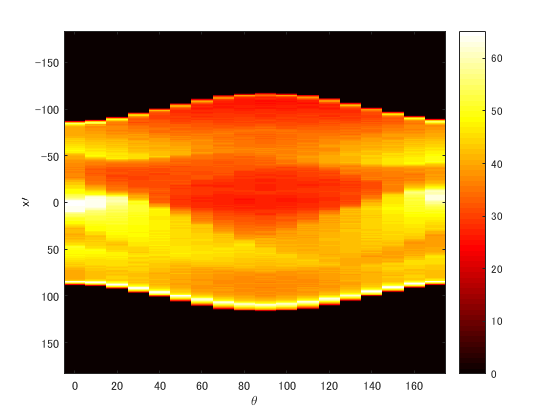
様々な方向からの投影が得られたと思います。
再構成方法
さて,Radon変換によって投影が得られました. では,投影からどうやって元の画像を復元するのでしょうか?
主に以下のような手法があります.
・投影切断面定理を用いる方法
・スパースモデリング
スパースモデリングは近年急速に流行っている手法なので,聞いたことがあるかもしれません。これらに関しては次の記事で説明していこうと思います。
【参考文献】
[1] X線CTとその応用
http://www.image.med.osaka-u.ac.jp/member/yoshi/mei_lecture/image_medicine/handout2007/naitoCT2007-2.pdf
[2]独立行政法人 国立病院機構 埼玉病院
http://saitama-hospital.jp/service/cardiovascular_province.html
[3] Matlab 逆ラドン変換
https://jp.mathworks.com/help/images/the-inverse-radon-transformation.html